Lightspeed and AntiGravity .
Andre Willers
18 Jan 2015
In honour of James Blish .
Synopsis :
We derive the General AntiGravity equations and indicate
some applications .
Discussion :
1.Spindizzy :
Big G http://en.wikipedia.org/wiki/Gravitational_constant can be manipulated , and has a singularity .
The
relevant equation is the Locke derivation of the Dirac-Brackett equation :
G = (2*c/b)
^2 * (L/s)^2
Where
G=Gravitational
Interaction between particles
c is
lightspeed , b~0.25 , s is magnetic moment , L is Angular Momentum .
See
Appendices below especially Appendix F .
S can be
written as a function of L
Therefore ,
if the above Dirac-Brackett equation holds , the Big G can be manipulated by
spinning the electron .Which we can do at will using laser tweezers or RF .
The
Solution (from Wolfram)
S=
-1/3(L-1) +- 3(2)^0.5 ( (L-2)
+3(3L-2)/(2L^2+3L+1) ) ^0.5 *(KK/n^3) , where kk is a constant and n is
primary quantum number .
Plugging it
into G above :
G= (2c/b )^2 * L^2/=
(-1/3(L-1) +- 3(2)^0.5 ( (L-2)
+3(3L-2)/(2L^2+3L+1) ) ^0.5 *(KK/n^3))^2 , where kk is a constant and n
is primary quantum number .
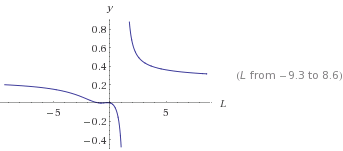
G then
looks like the picture below this before deviding by a constant (n^6/kk^2)
Where kk=1/2*Z^4*u(0) / (4pi)*g(s)*u(B)*a(0)^3)
U(0) is vacuum permeability =µ0 = 4π×10−7
V·s/(A·m) ≈ 1.2566370614...×10−6 H⋅m−1 or N·A−2 or T·m/A or Wb/(A·m)
g(s) is quantum correction constant =
2.002319304… http://en.wikipedia.org/wiki/Gyromagnetic_ratio
u(B) is Bohr magneton 9.740 x 10^-24 J
T^-1 (joules per tesla)
Z =nuclear charge .
a(0) is
Bohr radius = 5.2917721092(17)×10−11 m
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
2.How G
changes with Spin .
This is
generally applicable . Just multiply with the applicable constant .
This goes a
long way to explain Big Bang inflation , as well as later perceived acceleration
of expansion .
There
exists a spin for any material that leads to a singularity in Gravitational
force .
Tractor and
Repulsors can be made .
Metamaterial
with the exactly right spin will be like Cavorite : an anti-gravity material , what
today is called the http://en.wikipedia.org/wiki/Accelerating_universe
Notice that
G is negative in the above graph for small positive spins .
The
singularity on the y axis is better known as charge .
A monopole
is then possible (spin increasing to asymptotic axis or decreasing to
asymptotic axis) .
Should be
easy to make . A chirp RF generator should do the trick .
I would
expect anomalies to occur near big phase radar arrays .
And so they
do .
ABSTRACT The propagation of ultrashort optical pulses in an AlGaAs
waveguide array is studied using frequency-resolved
optical gating measurements. In the nonlinear regime, the measurements show that the pulses at the output of the array evolve toward a set chirp value that is independent of the input chirp. Simulations reproduce the experimental results. The observations can be described as a fixed-point attractor on a chirp-intensity map.
optical gating measurements. In the nonlinear regime, the measurements show that the pulses at the output of the array evolve toward a set chirp value that is independent of the input chirp. Simulations reproduce the experimental results. The observations can be described as a fixed-point attractor on a chirp-intensity map.
Yeah , right .
This means that any chirp system tends to a
behaviour independent of input . So much for Free Will .
The Universe is full of different frequencies .
We can order them in chirp fashion by fiat . But still not get what we want .
In any
case , to find cavorite use Google Earth
magnetic and look for the signature as
in Appendix F images .
If you are
lucky , you might even snag a monopole . In which case you can name your price
. The first one ,in any case .
After that
, they will find them in steadily increasing frequency .
If you don’t
believe me , check the history of exoplanets .
Example :
KK(1) for
one charge = 6.9252 x 10^46
A quantum
condensate made up of n molecules orbiting in a closed circuit (ie a virtual
central charge of n at the center due to constraint of material .)
Every
particle in the ring is in faster than light contact with every other one
because a quantum condensate is entangled .
See
Appendix C .
The
feedback effects in highly connected networks follow power laws of the form
y=ax^p
We need
only consider p=mMoles/AvogradoNumber .
To put it
another way , you need about (6.952*10^46)^(1/(6.022*10^23)) ~ 1.962 moles of
material to show an effect .
The highest
temperature superconductor we know about is H2S
at 190 K under pressure . http://arxiv.org/abs/1412.0460
That is 34.08088*
1.962 = 66.8 gm of H2S under pressure at 190 K .
The predicted metallization pressure is 111 GPa, http://www.nature.com/srep/2014/141110/srep06968/full/srep06968.html
This is
high . But there are ways around it . Mainly pulse . Explosive pulses at below
190 K can form shaped circular currents that lock in superconducting H2S .
This is
not even difficult or expensive .
Ley
lines .
More
interesting , enstatite in its perovskite-structured polymorph , suitably doped
with H2S , can form superconducting channels .
Pressure
plus volcanic H2S .
Shades
of Ley-lines !
I did
not expect this .
Carbon
Nanotubes and graphene :
Both
can handle 111 GigaPascal pressures .
The
poor man’s superconductor :
Carbon nanotubes
and irregular graphenes .
Just
look around volcanoes .
Prediction
of room temperature superconducting material from the earth :
Look
around explosive volcanos that are diamond bearing .
In
other words , carbon , H2S ,high pressure in the 111 GPa range.
They
should be fairly commonplace . A few hours at a place like Cullinan should
yield a few grams of room-temperature superconductor .
Why
hasn’t it been found before ?
Nobody
looked .
Remember
buckyballs ? Nobody looked either, If they did , buckyballs and the rest could
have been discovered at least 300 years before .
You now should be able to build your own antigravity machine
.
But it will be cheaper and easier to go and dig up some
pockets of cavorite .
Or make your own , using dug-up cavorite as seeds .
This is possible because of the chirp-chaos attractor as
mentioned above .
Ho-Ho-Ho !
Cavorite can breed more cavorite . All you need is the seed
.
Happy hunting !
Andre
Xxxxxxxxxxxxxxxxxxxxxxxxxxx
Appendix A
http://arxiv.org/ftp/arxiv/papers/0905/0905.4830.pdf
Two dimensional characterization of space-momentum
entangled photon pairs
Martin Ostermeyer, Dietmar Korn, Dirk Puhlmann
University of Potsdam, Institute of Physics and Astronomy,
Karl-Liebknecht-Str. 24/25, 14476
Potsdam, Germany
*Corresponding author: oster@uni-potsdam.de
Abstract: Space momentum entangled photon pairs are
generated from type II parametric
down conversion in a beta barium borate crystal. The
correlations in the positions of
photons in the near field and far field planes with regard
to the generating crystal are
observed in both transverse dimensions using scanning fiber
probes. The space-momentum
correlation is characterized using a covariance description
for a bivariate normal
distribution and tested for non-separability with Mancini’s
criterion. The role of higher
order spatial modes to observe spatial entanglement between
the two photons is discussed.
xxxxxxxxxxxxxxxxxxxxxxxxxxxx
Appendix B
Photons that travel in free space slower
than the speed of light
Daniel Giovannini, Jacquiline Romero, Vaclav Potocek, Gergely Ferenczi, Fiona Speirits, Stephen M. Barnett, Daniele Faccio, Miles J. Padgett
(Submitted
on 14 Nov 2014)
That the
speed of light in free space is constant is a cornerstone of modern physics.
However, light beams have finite transverse size, which leads to a modification
of their wavevectors resulting in a change to their phase and group velocities.
We study the group velocity of single photons by measuring a change in their
arrival time that results from changing the beam's transverse spatial
structure. Using time-correlated photon pairs we show a reduction of the group
velocity of photons in both a Bessel beam and photons in a focused Gaussian
beam. In both cases, the delay is several microns over a propagation distance of
the order of 1 m. Our work highlights that, even in free space, the invariance
of the speed of light only applies to plane waves. Introducing spatial
structure to an optical beam, even for a single photon, reduces the group
velocity of the light by a readily measurable amount.
Xxxxxxxxxxxxxxxxxxxxxx
Appendix
C
Bounding
the speed of ‘spooky action at a distance’
Juan Yin,
Yuan Cao, Hai-Lin Yong, Ji-Gang Ren, Hao Liang, Sheng-Kai Liao, Fei Zhou,
Chang
Liu, Yu-Ping Wu, Ge-Sheng Pan, Qiang Zhang, Cheng-Zhi Peng and Jian-Wei Pan1
1Shanghai
Branch, National Laboratory for Physical Sciences at Microscale,
and
Department of Modern Physics,
University
of Science and Technology of China, Shanghai 201315, China
Abstract
In the
well-known EPR paper, Einstein et al. called the nonlocal correlation in
quantum entanglement
as
‘spooky action at a distance’. If the spooky action does exist, what is its
speed?
All
previous experiments along this direction have locality loopholes and thus can
be explained
without
having to invoke any ‘spooky action’ at all. Here, we strictly closed the
locality loopholes
by
observing a 12-hour continuous violation of Bell inequality and concluded that
the lower bound
speed of
‘spooky action’ was four orders of magnitude of the speed of light if the
Earth’s speed in
any
inertial reference frame was less than 10−3
times of
the speed of light.
Vsa bigger than or equal 13800 *c
Where Vsa
is speed of Spooky Action
And c is
classical plane speed of light in vacuo .
xxxxxxxxxxxxxxxx
Appendix
D
Newton’s
Laws
|
First law:
|
When viewed in
an inertial reference frame, an object
either remains at rest or continues to move at a constant velocity,
unless acted upon by an external force.[2][3]
|
|
Second law:
|
The vector sum of
the forces F on an object is equal to the mass m of that object multiplied by the acceleration vector a of the object: F = ma.
|
|
Third law:
|
When one body exerts
a force on a second body, the second body simultaneously exerts a force equal
in magnitude and opposite in direction on the first body.
|
Xxxxxxxxxxxxxxxxxxxxxxx
Appendix E
Viewing a magnetic dipole as a rotating charged particle brings
out the close connection between magnetic moment and angular momentum. Both the
magnetic moment and the angular momentum increase with the rate of rotation.
The ratio of the two is called the gyromagnetic ratio and is simply the half
of the charge-to-mass ratio.[4] [5]
For a spinning charged solid with a uniform charge density to
mass density ratio, the gyromagnetic ratio is equal to half the charge-to-mass ratio. This implies that a more
massive assembly of charges spinning with the same angular momentum will
have a proportionately weaker magnetic
moment, compared to its lighter counterpart. Even though atomic particles
cannot be accurately described as spinning charge distributions of uniform
charge-to-mass ratio, this general trend can be observed in the atomic world,
where the intrinsic angular momentum (spin)
of each type of particle is a constant: a small half-integer times
the reduced Planck constant ħ. This is the
basis for defining the magnetic moment units of Bohr magneton (assuming charge-to-mass ratio of the electron)
and nuclear magneton (assuming charge-to-mass ratio of the proton).
Mass-to-charge ratio
From Wikipedia, the free encyclopedia
(Redirected from Charge-to-mass ratio)
Beam
of electrons moving in a circle in a Teltron tube,
due to the presence of a magnetic field.
Purple light is emitted along the electron path, due to the electrons colliding
with gas molecules in the bulb. The mass-to-charge ratio of the electron can be
measured in this apparatus by comparing the radius of the purple circle, the
strength of the magnetic field, and the voltage on the electron gun. The mass
and chargecannot be separately measured this
way—only their ratio.
The mass-to-charge
ratio (m/Q) is a physical
quantity that is most widely used in the electrodynamics of
charged particles, e.g. in electron optics and ion optics.
It appears in the scientific fields of electron microscopy, cathode ray
tubes, accelerator physics, nuclear physics, Auger spectroscopy, cosmology and mass
spectrometry.[1] The importance of
the mass-to-charge ratio, according to classical electrodynamics, is that two
particles with the same mass-to-charge ratio move in the same path in a vacuum
when subjected to the same electric and magnetic fields. Its SI units are kg/C.
Some
fields use the charge-to-mass ratio (Q/m)
instead, which is the multiplicative inverse of the
mass-to-charge ratio. The 2010 CODATA recommended value for an electron is e⁄me = (1.758820088±39)×1011 C/kg.[2]
Xxxxxxxxxxxx
Appendix F
Really interesting .
Spin–orbit interaction
In quantum physics, the spin–orbit interaction (also
called spin–orbit effect or spin–orbit coupling)
is an interaction of a particle's spin with its motion. The first and best known example of
this is that spin–orbit interaction causes shifts in an electron's atomic energy levels due to electromagnetic interaction between the
electron's spin and the magnetic field generated by the electron's orbit around
the nucleus. This is detectable as a splitting of spectral lines. A similar effect, due to the relationship between angular momentum and thestrong
nuclear force, occurs for protons and neutrons moving inside the nucleus, leading to a shift in their energy levels in the nucleusshell
model. In the field of spintronics, spin–orbit effects for electrons in semiconductors and other materials are explored for technological
applications. The spin–orbit interaction is one cause of magnetocrystalline
anisotropy.
The total spin–orbit potential in an external electrostatic
potential takes the form
The net effect of Thomas precession is the reduction of the
Larmor interaction energy by factor 1/2 which came to be known as the Thomas
half.
This leads to
We can now say
where
Where
n (the "principal quantum number") j (the "total angular
momentum quantum number"), L (the "orbital angular momentum quantum
number"), s (the "spin quantum number"),
As a wild approximation (since I have no
reputation)
Set j = (L+s)/2 . Reminiscent of Heron’s area
of the triangle .
We are essentially determining the “height”
into an unknown dimension using Heron’s formula . See
http://en.wikipedia.org/wiki/Heron%27s_formula
This gives an extraordinary result .
A mathematical island . The equivalent of a
particle
FunctionW
= ((L+s)/2((L+s)/2+1) – L(L+1) – s(s+1))
/ (L(L+1/2)(L+1))
Using Wolfram , this functionW looks like this
:
Notice the island formed by L the mass spin and
s the charge/magnetic effects of spin .
See below for the contour plot . Notice the
asymmetry .
So much for String Theory .
This Universe is inherently asymmetrical .
Built in at the pi level .
There is charge and energy level separation at
every scale .
Xxxxxxxxxxxxxxxxxxx
Appendix
G
See
pressures :
|
24 to 110 GPa
|
Stability range of enstatite in
its perovskite-structured polymorph,
possibly the most common mineral inside the Earth[citation needed]
|
||
|
40 GPa
|
|||
|
48 GPa
|
|||
|
69 GPa
|
10,000,000 psi
|
||
|
96 GPa
|
|||
|
1011 Pa
|
100 GPa
|
||
|
130 GPa
|
|||
|
> 300 GPa
|
|||
|
360 GPa
|
|||
|
1012 Pa
|
5 TPa
|
Pressure generated by the National Ignition Facility fusion
reactor.
|
|
|
1013 Pa
|
|||
|
1014 Pa
|
540 TPa
|
||
|
1015 Pa
|
6.5 PPa
|
||
|
1016 Pa
|
25 PPa
|
||
|
57 PPa
|
|||
|
1029 Pa
|
2.3×1029 Pa
|
||
|
1034 Pa
|
0.3 to16×1034 Pa
|
||
|
10113 Pa
|
4.6×10113 Pa
|
6.7×10109 psi
|
The Planck pressure (4.63×10108 bar), not reached except shortly after the Big Bang or
in a black hole[citation needed
|


No comments:
Post a Comment